优化算法是机器学习中的“方法论”,优化算法会告诉机器应该如何优化学习的进程,让自己能够更好地掌握学习到的知识,本文将针对机器学习领域中常用的几种优化算法进行总结。
梯度下降法
梯度下降法与梯度、导数的概念
梯度下降法是用来求解无约束优化问题的一种数学方法,通过梯度下降法可以获取到函数的局部极小值。这里存在一个概念“梯度”,梯度的本意实际上是一个向量,及具有方向性和数值性,其表示的是一个函数在改点沿着该方向变化最快(这个方向是往函数值变大的方向),这个变化率实际上就是该梯度的模。因此,在使用梯度下降法的时候,实际上是要求我们选择梯度的反方向进行计算,只有这样才能保证我们能够取到极小值,这也就是为什么在使用导数(导数与梯度实际上是同一个概念,只不过梯度是一种抽象的表述概念,而导数是实际上用来求解梯度的一种数学表示方式,导数值前面的正负号实际上是决定了梯度的方向)进行参数迭代的时候是要在导数的前面加上负号。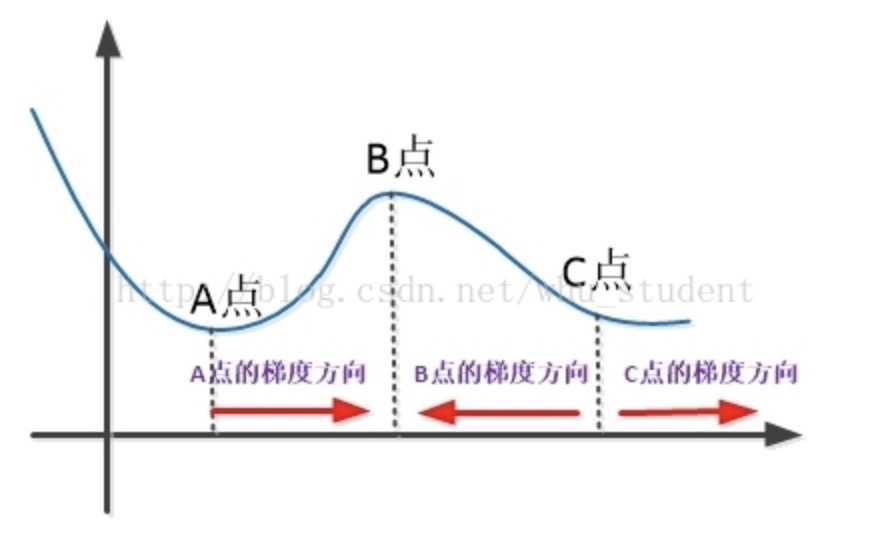
如上图所示,我们对函数f在A点对自变量x求解右导数$f^\prime$,其值为正数,那是因为在A点右侧函数值是增大的,因此,如果要想f值变小,则需要让往左移$x=x_a-\delta f^\prime$;对B点求解右导数,其值为负数,那是因为在B点右侧函数值是变小的,因此,如果想要f值变小,则需要让x往右移$x=x_a-\delta f^\prime$,因此,如果是要使用梯度下降法,则在迭代过程中要在导数的前面加上负号。
梯度下降法详解
应用前提条件
首先,我们得需要明确梯度下降法并不是万能的,因为在机器学习领域中,存在一个叫做NFL(No Free Launch)定理,这个定理说明了不存在一种模型或者算法能够适应于所有的应用场景。那么既然如此,梯度下降法能够应用于哪些场景中呢。其实从梯度下降法的原理来看,只要我们沿着梯度方向能够寻找到合适的最小值,那么就可以使用梯度下降法,那么如何判断什么样的函数是满足梯度下降法的应用的呢,最简单的一种方法就是判断该函数是否是下凸函数,如果一个函数是下凸函数,那么我们就可以针对该函数使用梯度下降法来求解最小值。当然,对于下凸函数可能会存在很多个局部极小值点,那么在这种情况下,使用梯度下降法来求解函数的最小值可能会存在一些偏差,那么此时,会通过一些技术性的措施(比如:采用随机性,分别从不同起始点多次进行梯度下降求解等)来优化我们使用梯度下降法的过程。
在梯度下降法中,通常需要优先确定以下条件:
1. 步长,也成为学习率 $\alpha$
2. 目标函数(损失函数,但是在确定损失函数过程$ L(\theta) $,需要优先确定模型$ h\_\theta(x) $)
基于上述两点先决条件,可以获得梯度下降法中最关键的表达式:
$ \theta_t = \theta_{t-1}-\alpha \frac{\partial L}{\partial x} $
下面将分别基于线性回归模型来阐述代数形式和矩阵形式下的梯度下降法。
梯度下降法的代数形式表达
- 假设有一组数据集$(x_1^1,x_2^1,…,x_n^1,y^1),(x_1^2,x_2^2,…,x_n^2,y^2),…,(x_1^m,x_2^m,…,x_n^m,y^m)$,该数据集共有m个样本,每个样本包含有n个特征量。
如果我们想通过线性回归模型来构建$x$与$y$之间的关系,可得如下模型:$h_\theta(x_1,x_2,…,x_n)=\theta_0+\theta_1 x_1 + … + \theta_n x_n$, - 采用线性模型常用的误差平方和作为损失函数L:
$L(\theta_0,theta_1,…,theta_n)=\frac{1}{2m}\sum_{j=1}^m(y_j-h_\theta(x_1^j,x_2^j,…,x_n^j)^2)$ - 使用梯度下降法求解,需要初始化相关参数,主要包含了$\theta$、$\alpha$、以及迭代停止距离$\epsilon$,通常我们可以将$\alpha$设置为0.9,$\theta$设置为0。
- 算法流程如下:
Step1:计算当前$L(\theta_0,\theta_1,…,\theta_n)$关于每个$\theta_i$的梯度:$\frac{\partial L}{\partial \theta_i}$;
Step2:用步长$\alpha$乘以Step1中求得的每个关于$\theta_i$的梯度,得到每个$\theta_i$下降的距离$d_i$;
Step3:判断每个$\theta_i$的梯度下降距离$d_i$的值是否都小于终止条件$\epsilon$,如果是,则停止学习,将当前的学习到的所有的$\theta_i$作为最终习得的参数,反之,进入Step4;
Step3:更新所有的$\theta_i$,更新公式如下:$\theta_i=\theta_i-\alpha \frac{\partial L}{\partial \theta_i}$,然后重复Step1~Step3.梯度下降法的矩阵形式表达
梯度下降法的矩阵表达形式实际上上对代数形式的矩阵话,为什么需要矩阵化?因为在实际的计算过程中,矩阵运算的效率与高于循环计算的效率,能够提升学习的效率。
通常我们会将样本数据集表示为$\matrix{X_{m \times n}}$,其中,$m$表示样本的个数,即矩阵的每一行表示一个样本信息,$n$表示样本中的特征量的个数,即矩阵中的每列表示的是一个特征量的取值。并且通常在机器学习领域中将向量表示为列向量,因此,所有的参数$\theta_i$可以表示为向量$\vec{\theta}$.
根据上述定义的矩阵和向量信息,可以重新表达线性模型:$\vec{y}=\matrix{X}\theta$,同时,损失函数可以表示为:$L(\theta) = \frac{1}{2}(\vec{y}-\matrix{X}\theta)^T(\vec{y}-\matrix{X}\theta)$,预先设置的参数步骤和代数形式是一致的,算法过程也是一致的,唯一的区别是在计算过程中变成了矩阵话运算。
梯度下降法的变形
上文所阐述的梯度下降法实际上是在每一轮迭代的过程中针对所有的样本进行梯度计算与梯度下降判断的,也可以成为全批量梯度下降法(Batch Gradient Descent),这样的方法具有以下缺点:如果样本量非常大的时候,计算的效率会降低,但是也具有准确率高的优点;
针对BGD算法效率低的问题,又提出了一种随机梯度下降法(Stochastic Gradient Descent),顾名思义,这种做法是每一轮迭代都只随机选取一个样本进行计算,这种方式大大提升了计算的效率,但是,由于每一次都是随机选取一个样本进行迭代计算,那么会导致获得的参数值并不是局部最优解,同时,这样方式还会导致每次迭代时的方向会不稳定,即整体的收敛速度会下降;
针对上述两种极端的梯度下降法,又提出了一种小批量梯度下降法(Mini-Batch Gradient Descent),这种方法通常是选择部分样本参与计算,通常每轮迭代选择的样本量为16,32,64,128,256,512等这类$2^n$的值。(Notes:在机器学习中,如果样本量过大的时候,我们通常会在没一轮的学习过程中选择部分样本来参与学习,同时增加学习的轮数,这样可以通过多次学习的方式,来提升每次训练的效率,并且因增加了学习的次数,也能够从整体上降低泛化误差)。
梯度下降法应用场景
损失函数必须是凸函数,即存在局部极小值点
基本牛顿法
牛顿-拉夫森法
基本牛顿法在优化问题中的应用实际上是来源于牛顿-拉夫森法,该方法是用来求解函数的零点的方法,那么这个方法到底是什么方法呢,实际上,该方法是建立在泰勒展开公式的基础上,通过使原方程泰勒展开的一阶近似等于零不断获得更好的结果的求解方程零点的方法。简单来说,具有以下特点:
1. 牛顿法是求解方程零点的方法
2. 牛顿法利用泰勒展开的一阶近似的零点获得更接近真实零点的点
3. 牛顿法通过迭代的方法不断的获得更好的解来求得最好的解
首先,假设存在一个函数$f(\vec{x})$,那么利用泰勒展开公式,将其进行一阶泰勒展开$f(\vec{x})=f(\vec{x_0})+\frac{\partial f(\vec{x})}{\partial \vec{x}}|{\vec{x}=\vec{x{0}}}(\vec{x}-\vec{x_0}))$,我们可以求解出展开式的零点,即令
$$
\begin{split}
& f(\vec{x_0})+\frac{\partial f(\vec{x})}{\partial \vec{x}}|{\vec{x}=\vec{x{0}}}(\vec{x}-\vec{x_0}))=0 \
=> & \vec{x}_1=\vec{x_0}-\frac{f(\vec{x_0})}{\frac{\partial f(\vec{x})}{\partial \vec{x}}|_{\vec{x}=\vec{x_0}}}
\end{split}
$$
然后再在$\vec{x}_1$处进行一阶泰勒展开,如此迭代求解,可以计算得到:
$$
\vec{x}n=\vec{x{n-1}}-\frac{f(\vec{x_{n-1}})}{\frac{\partial f(\vec{x})}{\partial \vec{x}}|{\vec{x}=\vec{x{n-1}}}}
$$
然后判断$f(\vec{x_{n-1}})<\epsilon$,如果满足,则停止迭代,说明此时的$\vec{x}_{n-1}$就是函数$f(\vec{x})$的零点。
基本牛顿优化法
当我们需要求解一个函数的极值点点的时候,最重要的判断条件就是$\frac{\partial f}{\partial \vec\theta} = 0$,也就是函数的一阶导数为0时所对应的点。那么,如果要用牛顿法来解决最优化的问题,最根本的问题就是,使用牛顿-拉夫森方法来求解$\frac{\partial f}{\partial \vec\theta}$的零点。
首先,我们对函数进行二阶泰勒展开:
$
\begin{split}
& f(\vec{x})=f(\vec{x_0})+\frac{\partial f(\vec{x})}{\partial \vec{x}}|{\vec{x}=\vec{x{0}}}(\vec{x}-\vec{x_0}))+\frac{1}{2}\frac{\partial ^{2} f(\vec{x})}{\partial ^{2} \vec{x}}|{\vec{x}=\vec{x{0}}}(\vec{x}-\vec{x_0})^{2}) \
\end{split}
$
对上述公式求导:
$$
\begin{split}
& \frac{\partial f(\vec{x})}{\partial \vec{x}}= &\frac{\partial f(\vec{x})}{\partial \vec{x}}|{\vec{x}=\vec{x{0}}} + \frac{\partial ^{2} f(\vec{x})}{\partial ^{2} \vec{x}}|{\vec{x}=\vec{x{0}}}(\vec{x}-\vec{x_0}) \
=> & \vec{x}n=\vec{x{n-1}}-\frac{f(\frac{\partial f(\vec{x})}{\partial \vec{x}}|{\vec{x}=\vec{x{n-1}}}}{\frac{\partial^{2} f(\vec{x})}{\partial^{2} \vec{x}}|{\vec{x}=\vec{x{n-1}}}}
\end{split}
$$
因此,由上述公式可知,我们可以通过函数的一阶导数和二阶导数不断迭代计算出$\vec{x}$,
然后判断$\frac{\partial f(\vec{x})}{\partial\vec{x}}|{\vec{x}=\vec{x{n-1}}}<\epsilon$,如果满足,则停止迭代,说明此时的$\vec{x}_{n-1}$就是函数$f(\vec{x})$一阶导数的零点。
在机器学习中,二阶导数就是海森矩阵。
牛顿法的优缺点
实际上牛顿法与梯度下降法在优化问题上的本质方法是一致的,唯一的区别是在于如何求解的问题,在牛顿法中的海森矩阵就相当于梯度下降法中的学习率(步长)。牛顿法收敛速度相比梯度下降法很快,而且由于海森矩阵的的逆在迭代中不断减小,起到逐渐缩小步长的效果。但是,如果样本量非常大,那么会导致计算海森矩阵的效率很慢,同时还需要大量的计算资源。
拟牛顿法
为了解决牛顿法中求解海森矩阵的问题,我们可以在满足拟牛顿条件的基础上构造一个近似的海森矩阵,用近似值来代替标准的海森矩阵参与计算。常用的近似计算算法有DFP算法,BFGS算法,L-BFGS算法以及Broyden类算法等。
//todo
最小二乘法
最小二乘法也是用来估计这样一种参数,该参数能够使得观测值和理论值之差的平方和最小,通常是用来优化线性模型,从最小二乘法的概念上可知,其应用的目标函数是非常受限的,也就是说,其优化的目标函数必须是服从以下形式的:
$L(\theta)=\sum_{i=1}^{m}{(y-y^h)}^2$.
为什么要用这个平方和来表示损失函数呢?什么是最小二乘法的理论基础呢?实际上,最小二乘法是符合矩阵投影理论和高斯正态误差理论的。
在深入理解最小二乘法之前,我们需要定义误差,如果从线性空间的角度来看的话,误差是什么?误差其实就是在空间中寻找两个向量之间的差值最小。如下图,我们可以假设$\vec{b}$是一个标准的值,那么如果存在一个特定的映射模型,将确定为$\vec{a}$,那么我们需要在$\vec{a}$这个向量中寻找出与$\vec{b}$误差最小的一个向量点,也就是$\vec{p}$.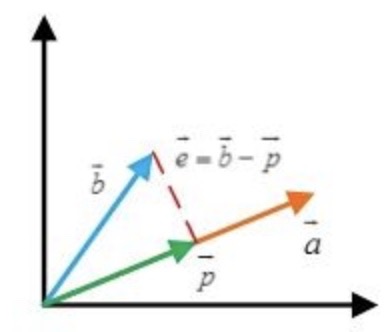
结合线性模型来理解的话,通常$\vec{y}$指的是空间中的一个向量,而线性模型中的参数向量实际上是一种变换,这种变换会将空间中的点$\matrix{X}$映射出$\vec{y^g}$,但是,由于我们通常是无法准确地获得$\matrix{X}$与$\vec{y}$之间的映射关系,一方面是因为数据测量的误差,另一方面是模型本身存在误差;因此,$\vec{y}$与$\vec{y}$之间是存在误差的。实际上,寻找最优模型实际上就是寻找最优的$\vec{a}$。
最小二乘法的矩阵表示形式
假设损失函数为$L(\theta) = \frac{1}{2}(\vec{y}-\matrix{X}\theta)^T(\vec{y}-\matrix{X}\theta)$,那么,根据最小二乘法原理,对$L$针对$\theta$求导,并将其赋值为0,从而求解出$\theta$的值。
$$
\begin{split}
\frac{\partial L}{\partial \theta}= &\frac{1}{2}\frac{\partial(\vec{y}^T\vec{y}-\vec{y}^T\matrix{X}\vec{\theta}-\vec{\theta}^{T}\matrix{X}^T\vec{y}+\vec{\theta}^T\matrix{X}^T\matrix{X}\vec{\theta})}{\partial \vec\theta} \
=&\frac{1}{2}(-\vec{y}^T\matrix{X}-\frac{\partial{(\vec{\theta}^{T}\matrix{X}^T\vec{y}})^T}{\vec{\theta}}+\vec\theta^T\matrix{X}^T\matrix{X}+\frac{\partial\theta^T }{\partial\vec{\theta}}\matrix{X}^T\matrix{X}\vec{\theta}) \
= & \frac{1}{2}(-\vec{y}^T\matrix{X}-\vec{y}^T\matrix{X}+\vec\theta^T\matrix{X}^T\matrix{X}+\frac{(\partial\vec\theta^{T} \cdot \matrix{X}^T\matrix{X}\vec{\theta})^T}{\partial\vec\theta}) \
= & \frac{1}{2}(-2\vec{y}^T\matrix{X} + 2\vec\theta^T\matrix{X}^T\matrix{X})=0
\end{split}
$$
基于上式,可以推导出$\vec\theta=(\matrix{X}^T\matrix{X})^{-1}\matrix{X}^T\vec{y}$
(Notes:一个函数的维度和该函数的微分的维度是保持一致的)
最小二乘法的应用场景
- 模型必须是线性模型,求解的损失函数是误差的平方和,(如果不是线性的,则需要通过非线性函数映射,将其映射为线性模型,eg:$g(\vec{y})=\matrix{X}\vec\theta$,令$h=g(\vec{y})$,则此时可以针对$\vec{h}$与$\matrix{X}$构建线性模型)
- $\matrix{X}^T\matrix{X}$必须要是可逆。
最大似然估计
最大似然估计法是统计学中一个用来求解参数模型中参数的方法,这种方法和前面的优化算法类似,也是要求具有明确的模型,然后根据观测的数据来求解模型中未知的参数。
最大似然原理
似然函数表示的是统计模型中关于参数的一种函数,这种函数表达的含义是参数的似然性(或者说该参数取某个值的概率性)。
在统计学中,假定存在一个分布$D$,并且假设该分布的概率密度函数(连续型)或者概率质量函数(离散型)为$f_\theta$,并且该函数是关于参数$\theta$的一个函数。那么我们独立地从该分布中抽取出$n$个数据,分别为$X_1,X_2,…,X_n$,那么,通过这n个观测的数据,我们可以计算出模型中参数$\theta$的似然函数,如下:
$lik(\theta|x_1,x_2,…,x_n)=f_\theta(x_1,x_2,…,x_n)$
由最大似然原理可知,要使用最大似然估计最重要的一点就是需要知道数据分布的概率密度函数或者概率质量函数,同时,该函数也是我们的建模函数,也就是说,我们针对一个特定的业务问题,通过构建关于该问题的概率密度函数或者概率质量函数模型,然后通过最大似然函数求解该模型中的参数,得到一个精确的函数。
最大似然估计法原理
基于最大似然原理可知,我们需要计算模型中的参数的时候,需要构建该参数的似然函数,那么怎么才能得到这个似然函数呢,最好的方式就是根据已知的观测数据,来计算这个似然函数,具体来说就是构建如下似然函数:
$f(x_1,x_2,…,x_n|\theta)$,显然,这是一个联合概率分布.
- 那么为了简化这个问题的计算过程,通常会假设所有的数据样本之间是独立的,因此,有如下表达式:
$f(x_1,x_2,…,x_n|\theta)=\prod_{i=1}^{n} f(x_i|\theta)$ - 同时,由于连乘计算不方便,因此,会对上述公式取对数,从而转变为加法计算,这样非常方便求解函数的极值点。
最大似然估计法最根本的就是求解$f(x_1,…,x_n)$的最大值。
最大似然估计法的步骤入下:
- 写出似然函数
- 对似然函数取对数,并整理;
- 求导数 ;
- 解似然方程
(Notes:最大似然估计只考虑某个模型能产生某个给定观察序列的概率,而未考虑该模型本身的概率)